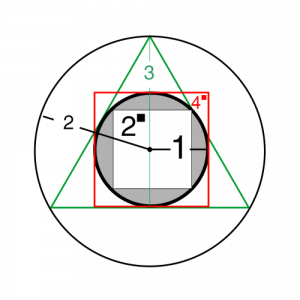
Die nebenstehende geometrische Abbildung zeigt die lineare Folge der Zahlenarchetypen 1, 2, 3, 4 alias Kreis, Dreieck und Quadrat auf geometrische Weise aufeinander bezogen. Dennoch erkennen wir zwischen ihnen keinen einfachen, zusammenhängenden Algorithmus. Unsere linearlogische Betrachtung läuft ins Leere. Wenn wir die Abbildung zunächst jedoch nur als eine Zusammenstellung von geometrischen Figuren betrachten und jeweils immer nur paarweise eine spezifische Beziehung inhaltlich hinterfragen, entsteht aufgrund des Wissens um das Wesen der Archetypen ein Bild der Einheit.
Die paarweise Betrachtung, d.h. der Bezug jeweils zweier Archetypen zueinander erhellt in besonderer Weise deren Qualitäten. Am Beispiel des Einheitskreises und seines inneren Quadrates (s. Abb. „Einheitskreis„) habe ich das für das Verhältnis von 1—2 bereits ausgeführt. Das Beispiel hatte gezeigt, dass der Archetyp der ZWEI das Prinzip des BRUCHs beschreibt und die profane Vorstellung von Linearität korrigiert. Jeder neue Archetyp ist ein solcher, weil er den Bruch auf seine spezifische Weise neu erzeugt. Das führt zu einem neuen Verstehen der Zahlen, das deren Abfolge als eine Abfolge von Archetypen begreift. In ihr hat die Linearität keinen Selbstzweck, sondern steht ganz im Dienst der Archetypen. Das soll die obenstehende Abbildung zeigen. Obwohl sie die ersten vier Archetypen in ihrem geometrischen Bezug zueinander enthält, eröffnet der Bezug zwischen ihnen keinen einfachen Algorithmus, wie wir ihn aus der Zahlenfolge, die durch das immerwährende „plus 1“ entsteht, kennen.
Es ist der immer erneute Bruch zwischen den Archetypen, der uns zwingt, aus der Abbildung heraus immer nur das Verhältnis von zwei Archetypen zueinander zu betrachten und das Gesamtbild zunächst nur als eine Zusammenstellung von Gegensätze anzusehen. Erst später lassen sich daraufhin dann auch größere Strukturen, wie beispielsweise die im pythagoreischen Dreieck schon vorgestellte Beziehung von Geist (3) und Substanz (4) in ihrem gemeinsamen Bezug zum Einheitskreis (1) erkennen. Bis dahin verraten uns die in der Abbildung enthaltenen Einzelbeziehungen mehr über deren Wesen:
Der Archetyp Drei alias das Dreieck verbindet die in der Linearität erscheinenden Gegenpole miteinander. Die „Funktion“ im Sinne des Verbindens ist sein Wesen. Das zeigt die Abbildung, denn das Dreieck ist die Figur, die den Kreis des Radius 1 mit dem Kreis des Radius 2 verbindet. Das geht nur mit dem Dreieck. Dieses, sein Wesen tritt auch in der Umkehrung zutage. Der Kreis verbindet das Dreieck der Höhe 1 mit dem Dreieck der Höhe 2. Auch das funktioniert nur mit dem Dreieck.

Abb. 4:
(li) Das Dreieck verbindet die Kreise r = 1 und r = 2 miteinander
(re) Der Kreis verbindet die Dreiecke h = 1 und h = 2 miteinander.
Das den Einheitskreis umgebende Quadrat der Fläche 4 erinnert uns an die zwiespältige Beziehung der beiden geometrischen Figuren. Das allbekannte unlösbare Problem der Quadratur des Kreises verweist auf den Widerspruch zwischen Rationalität und Irrationalität indem es uns zeigt, dass es nicht möglich ist, ein Quadrat mit dem exakt gleichen Flächeninhalt eines Kreises zu konstruieren. Den tieferen inhaltlichen Zusammenhang haben wir im Wesen des Bruchs über die Beziehung des vom Einheitskreis umfangenen/eingeschlossenen Quadrats der Fläche 2 zu ihm kennengelernt. Dieses „innere Verhältnis“ gibt uns die Deutungsvorlage für alle konkreten Erscheinungen in den Substanzen.
Alle Erscheinungen nehmen wir als Oberflächen war. Sie sind „äußere Erscheinungen“. Unter diesem Aspekt müssen wir die Beziehung vom inneren und äußeren Quadrat des Einheitskreises betrachten. Das den Einheitskreis umschließende, äußere Quadrat hat die Fläche 4. Das Quadrat zeigt als ein eigener, von der Einheit unterschiedener Archetyp dessen manifestierten Inhalt in Form einer rational erscheinenden Oberfläche an.
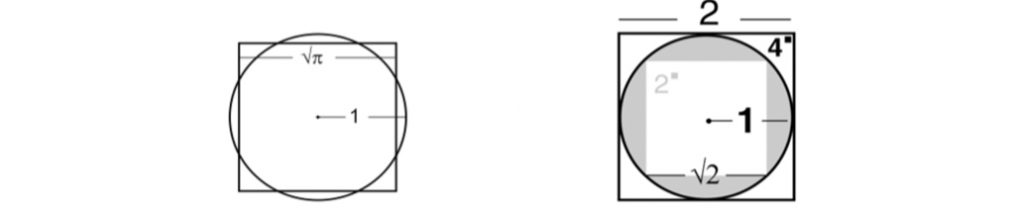
Abb. 5:
(li) Die Unmöglichkeit der „Quadratur des Kreises“ begründet sich im Bruch wischen Rationalem und Irrationalem.
(re) Der den Einheitskreis konstituierende Parameter (r = 1) ist auch der, welcher das Vierquadrat (a = 2) konstituiert. Sie sind über die gleiche, lineare Logik auseinander abzuleiten.
Die Vier ist die Zahl der sichtbaren Vollkommenheit – der Logos. Das in der Vierzahl erscheinende Wunder besteht darin, dass es einstige Gegensätze ganzheitlich manifestiert. War das vom Einheitskreis umfasste Quadrat auf linearlogische Weise noch nicht mit der sie erzeugenden Größe (Einheit) in Einklang (Kreis) zu bringen, so ändert sich das in dem den Einheitskreis umschließenden Vierquadrat. Den Gegensatz von Rationalität und Irrationalität, wie er uns in der Unmöglichkeit der Quadratur des Kreises vor Augen führt, erkennen wir auch im Vierquadrat. Doch illustriert dieses äußere Quadrat zugleich auch die Einheit der Parameter, welche die unterschiedenen Figuren charakterisieren. Das (Seiten-)Maß des Quadrats (a = 2) hat den gleichen Maßstab wie der Radius (r = 1), der den Kreis hervorbringt. Das war bei dem im Einheitskreis eingeschlossenen Quadrat noch anders. Dort standen sich noch r = 1 und a = √2 linearlogisch unvereinbar gegenüber.
Die Vier ist der Logos. Ihre Botschaft ist: Sie manifestiert die einstigen Gegensätze als sichtbare Ganzheit, ohne die sie ausmachenden Qualitäten zu zerstören.
